

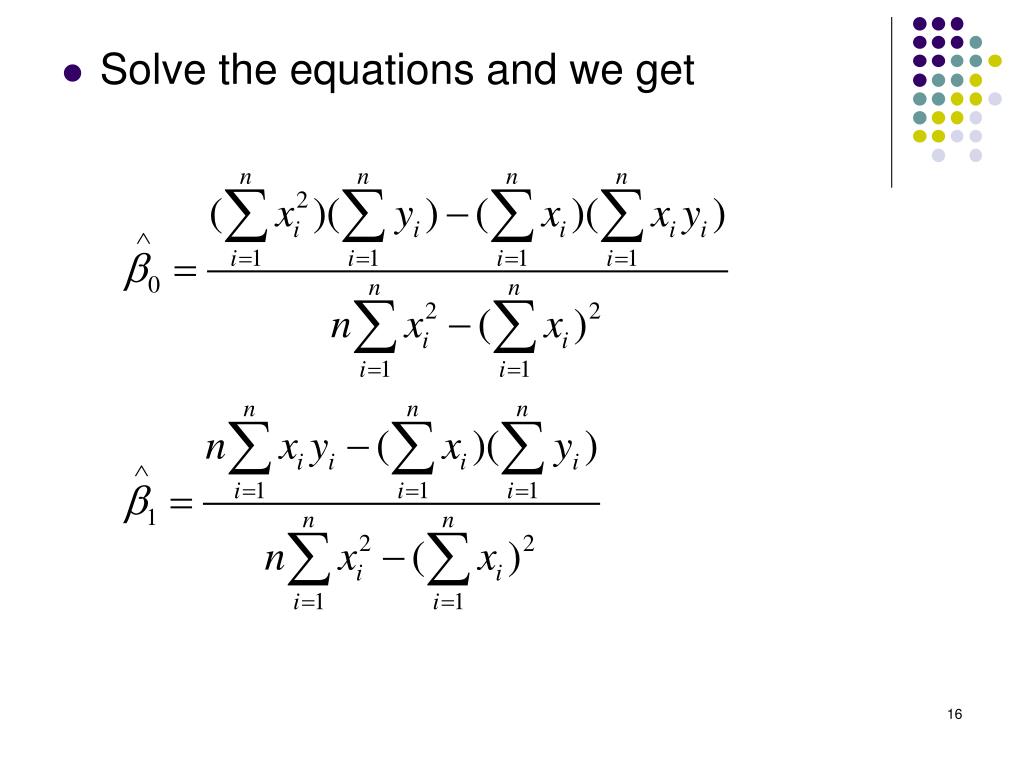
r near +/-1 -> strong association T/F: correlation is not causation TRUE A correlation coefficient of r=.75 is reasonable for a linear regression equation relating hair color, to weight False - hair color is not numerical If R^2 =.81, then R=.9 FALSE - the. slope If X= the month you were born in (1.,12) and Y=your height (inches), what r would I get if I collected data and computed the correlation? very close to 0, but not necessarily exactly 0 (due to sampling error) If the p-value (for the slope) on a regression printout = 0.00001 then.ĩ. The simple linear regression (least squares method) minimizes: SSE = SS(Residuals) When x=0 intercept R square percentage variance explained SS(regression) + ss(residual) SS(total) increasing relationship direct _ has same sign as correlation slope beta error 2 decision when not convincing information accept null status quo assumption null SS of prediction errors SS(residual) correlation straight line association rho population correlation covariance numerator of correlation regression trend line decreasing relationship inverse alpha error 1 If the _ of the computed regression line is 0 then we can conclude that r = 0.


 0 kommentar(er)
0 kommentar(er)
